Widmo ciągłe

W przypadku fal nieokresowych i innych sygnałów niestacjonarnych, widmo nie zawiera dyskretnych prążków (ponieważ nie występuje okresowość) lecz jest ciągłą funkcją w dziedzinie częstotliwości. Sygnału takiego nie można wyrazić sumą szeregu harmonicznego, lecz przez całkę z jego widma obliczoną w ciągłym przedziale częstotliwości: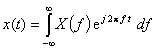

Widmo ciągłe X(f) może być wyznaczone z sygnału w dziedzinie czasu x(t) przez zastosowanie transformacji Fouriera (całkowego przekształcenia Fouriera):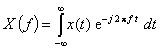

Wynik tego przekształcenia, czyli transformata Fouriera, jest w ogólności ciągłą funkcją, która opisuje udział drgań o wszystkich częstotliwościach w sygnale x(t). Przykładowo, krótkie impulsy i przebiegi stanów nieustalonych (tzw. transienty) mają zazwyczaj szerokie widmo, gdyż znacząca część ich energii zawarta jest w drganiach składowych o wysokich częstotliwościach.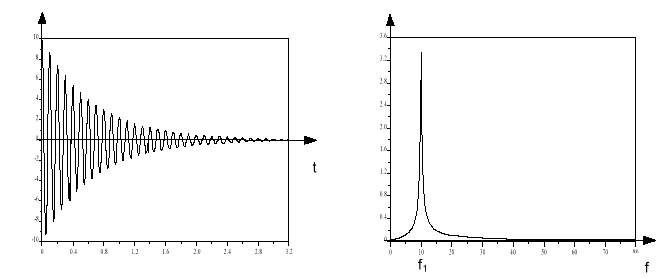

Przykład sygnału transientowego i jego ciągłe widmo X(f)

Więcej o przekształceniu Fouriera można dowiedzieć się z [2,3,4] .