Analiza widmowa sygnałów dyskretnych

Kilka wariantów przekształcenia Fouriera zostało zdefiniowanych dla sygnałów dyskretnych. Najbardziej popularna Dyskretna Transformacja Fouriera (DFT) analizuje ciąg próbek sygnału o skończonej długości N: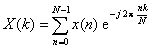

,

gdzie x(n) oznacza n-tą próbkę, a k=0..N-1

W wyniku skończonej długości ciągu {x(n)} oraz okresowości jądra przekształcenia e^-jkn2π/N, również widmo X(k) jest okresowe. Wartości X(k) reprezentują widmo fragmentu sygnału x(n) spróbkowane w N dyskretnych punktach w dziedzinie częstotliwości: 0, f_s/N, 2f_s/N, 3f_s/N ... (N-1)f_s/N. Możliwe jest odtworzenie sygnału w dziedzinie czasu x(n) przy pomocy transformacji odwrotnej: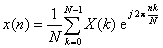

O ile bezpośrednia implementacja powyższych transformacji wymaga o(N²) operacji mnożenia i sumowania, to jednak istnieje wiele metod efektywnego obliczania DFT i DFT^-1. Najbardziej popularne pośród nich Szybkie Przekształcenie Fouriera (FFT) wymaga jedynie o(N log₂N) operacji. FFT jest jednym z najbardziej nieodzownych i powszechnie stosowanych algorytmów współczesnego CPS [ ].