Podobnie jak w klasycznej teorii sygnałów jednowymiarowych, w teorii sygnałów wielowymiarowych rozróżnia się sygnały ciągłe i dyskretne. Sygnał ciągły jest reprezentowany funkcją zmiennych niezależnych przyjmujących wartości rzeczywiste, podczas gdy dla sygnałów dyskretnych argumenty takiej funkcji są całkowite. Dwuwymiarowy sygnał dyskretny reprezentuje obraz, który składa się z próbek o odpowiednio dobranych położeniach na płaszczyźnie obrazu. Typowa notacja ma postać:

gdzie n₁,n₂ są indeksami w poziomie i pionie (odpowiednio).

Jednowymiarowe przekształcenie Fouriera

Z klasycznej teorii sygnałów dobrze znane jest jednowymiarowe przekształcenie (transformacja) Fouriera sygnału, które można zdefiniować dla wielu sygnałów dyskretnych f(n):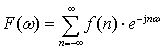

gdzie funkcję F(ω) nazywa się transformatą Fouriera sygnału f(n). Transformata rzeczywistego sygnału f(n) ma w ogólności zespolone wartości i jest okresową funkcją rzeczywistego argumentu ω, czyli pulsacji. Transformacja Fouriera jest wygodnym narzędziem analizy sygnałów, a także procesów transmisji sygnałów przez układy liniowe.

Jeżeli transformata F(ω) istnieje, to można dokonać transformacji odwrotnej: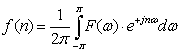

Powyższe wzory definiujące prostą i odwrotną transformację Fouriera można w dosyć oczywisty sposób uogólnić na sygnały dwuwymiarowe.