Dwuwymiarowe przekształcenie Fouriera

Obraz nieruchomy jest reprezentowany przez sygnał dwuwymiarowy, dla którego można określić dwuwymiarową transformatę Fouriera: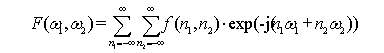

Przekształcenie odwrotne określa wzór: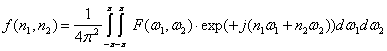

Dwuwymiarowe przekształcenie Fouriera jest operatorem, który sygnałowi dwuwymiarowemu f(n), gdzie n = [n₁, n₂]^T przyporządkowuje zespoloną funkcję F(ω) o N argumentach ω = [ω₁, ω₂]^T.

Dwuwymiarowe sygnały dyskretne spotykane w cyfrowym przetwarzaniu obrazów przeważnie spełniają następujące dwa warunki:

- przybierają tylko skończone wartości,

- wartości niezerowe przybierają tylko w skończonym obszarze, czyli: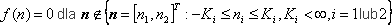

Dla dyskretnych sygnałów dwuwymiarowych f(n) spełniających te dwa warunki zawsze istnieje wielowymiarowa transformata F(ω). Jeżeli transformata istnieje, to przekształcenie Fouriera jest wzajemnie jednoznacznym przyporządkowaniem funkcji f(n) jej transformaty F(ω), co zapisuje się: f(n)) <-> F(ω).

Transformata Fouriera F(ω) sygnału dyskretnego jest okresowa względem obu swoich argumentów ω_i, i = 1, 2. Ze wzoru definicyjnego wynika, że okres wynosi 2π .