Finite Impulse Response filters

FIR (Finite Impulse Response) filter is defined by the following equation: 

	N1	N2
y (nx,ny)  =	Σ	Σ    h(kx,ky) • u(nx-kx,ny-ky)
	kx= - N1	ky= - N2

where: u( , ) is an input picture sample; y ( , ) is an output (filtered) picture sample; h( , ) is an impulse response sample.

The impulse response of a filter is its response to the input that contains only one nonzero sample with its value equal to one. The FIR filter is such a filter that its impulse response consists of a finite number of nonzero samples. These samples may be represented in a table [h(k_x,k_y)]. This table is often called filter mask.

Processing with FIR filter may be interpreted as filter mask sliding over input image and producing (by multiplying and summing) the output image samples. See the picture below for N₁ = N₂ = 2 example.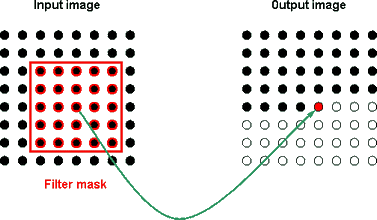