Similarly as classic signal theory, the theory of two-dimensional signals considers continuous and discrete signals. A continuous signal is represented as a function of real-valued independent variables, while these arguments are integer for discrete signals. A two-dimensional discrete signal represents an image that consists of samples located at appropriate positions at the image plane.

Typical notation for a discrete two-dimensional signal is

where n₁,n₂ are horizontal and vertical indices, respectively.

One-dimensional Fourier transform

The classic signal theory considers well-known one-dimensional Fourier transform that May be defined for many discrete signals f(n):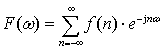

where the function F(ω) is called as the Fourier transform of the signal f(n). In general, a transform of a real-valued signal f(n) exhibits complex values and is a periodic function of a real argument ω, that is of radial frequency. The Fourier transform is a powerful tool for signal analysis as well a perfect tool of analysis of signal transmission by linear systems.

If a transform F(ω) exists, there exists an inverse transform: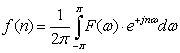

The above formulae define the forward and inverse Fourier transforms. They may be easy generalized onto two-dimensional signals.