Dyskretne dwuwymiarowe przekształcenie Fouriera

Dwuwymiarowe przekształcenie Fouriera definiuje się za pomocą sumy wyliczanej z wykorzystaniem nieskończonej liczby próbek oryginalnego sygnału. Obrazy w zasadzie mają skończone rozmiary i dlatego dla dokonania sumowania we wzorze definicyjnym transformaty należy obraz w pewien sposób uzupełnić w celu uzyskania sygnału o nieskończonej liczbie próbek. Na przykład obraz składający się z N₁•N₂ próbek można uzupełnić zerami, ale można też utworzyć z niego okresowy dwuwymiarowy sygnał o okresach N₁, N₂.

Ponadto należy zauważyć, że korzystając z N₁•N₂ próbek obrazu, za pomocą liniowego przekształcenia, jakim jest przekształcenie Fouriera, można wyliczyć co najwyżej N₁•N₂ niezależnych próbek widma.

Dwuwymiarowe dyskretne przekształcenie Fouriera jest określone wzorem: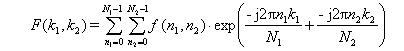

gdzie 0 < k₁, n₁ < N₁-1 oraz 0 < k₂, n₂ < N₂-1

Transformację odwrotną określa wzór: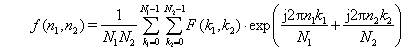

Dyskretne dwuwymiarowe przekształcenie Fouriera wzajemnie jednoznacznie odwzorowuje sygnał na jego transformatę, co zapisujemy podobnie jak dla samego przekształcenia Fouriera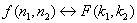

poprzednia strona wykładu

podsumowanie lekcji